The Theory of Special Relativity
BASIC PRINCIPLES, LIMITS, POSSIBLE AMENDMENTS AND SUGGESTIONS FOR DECISIVE EXPERIMENTSGerhard W. Borst
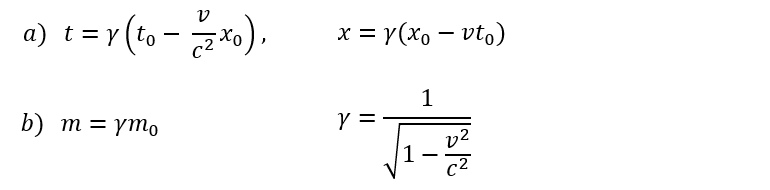
- Exchange of signals inside moving bodies (2.2)
- Exchange of signals and correlation of angles (2.3)
- Signal exchange in any spatial direction (2.4)
- Experiments with transparent media in motion (4.2)
- Triggering of engines after synchronization (4.3)
- Signal exchange between observers with spatial geometry (4.4)
- Clock transport t (5.1)
- Twin paradox (5.2)
- Relativistic mass increase and energy (6.1)
- Spring paradox (6.2)
- Relativistic elastic collision (6.3)
- Exchange of signals in systems with constant acceleration (6.4.1)
- Relativistic rocket equation (6.4.2)
- Relativistic non-elastic collisions (7.1)
- Analysis of disintegration into 2 particles (7.2.1)
- Disintegration into 2 photons (7.2.2)
- Invariance of phase velocity during transition between different inertial systems (8.)